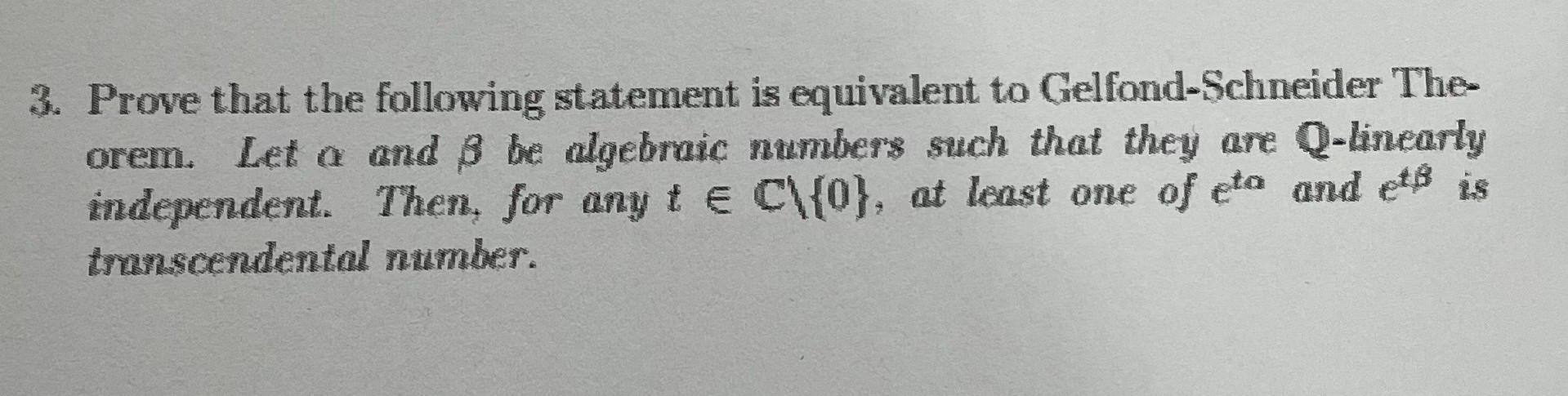Satz von Gelfond-Schneider

Der Satz von Gelfond-Schneider (englisch Gelfond-Schneider theorem) ist ein bedeutender Satz aus dem mathematischen Teilgebiet der Zahlentheorie. Mithilfe dieses Satzes konnte zum ersten Mal eine umfangreiche Klasse von transzendenten Zahlen erzeugt werden.

Der Satz wurde im Jahre 1934 von dem russischen Mathematiker Alexander Gelfond und unabhängig davon und nur wenig später von Theodor Schneider gefunden und bewiesen. Der Satz liefert die Lösung des siebten Hilbertschen Problems.

Aussage des Satzes

Der Satz von Gelfond-Schneider besagt:

Es seien

\alpha

und

\beta

zwei komplexe Zahlen, die zudem algebraisch seien, wobei

\alpha \neq 0,1

gelten soll und darüber hinaus

\beta \in {\mathbb {C} \setminus \mathbb {Q} }

sei.

Dann ist

\,\alpha ^{\beta }

transzendent.

Er lässt sich auch so formulieren, dass für Logarithmen zweier algebraischer Zahlen aus der linearen Unabhängigkeit über den rationalen Zahlen die lineare Unabhängigkeit über den algebraischen Zahlen folgt. In dieser Formulierung ist der Satz von Gelfond-Schneider in den 1960er Jahren von Alan Baker erheblich erweitert worden.

Der Satz von Baker lautet:

Wenn endlich viele algebraische Zahlen

a_{i}\neq 0\,(i=1,2,\ldots ,n;n\in \mathbb {N} )

vorliegen, so dass

\log a_{1},\ldots ,\log a_{n}

über den rationalen Zahlen linear unabhängig sind, dann sind

1,\log a_{1},\ldots ,\log a_{n}

auch linear unabhängig über den algebraischen Zahlen.

Anwendungen

Aus dem Satz von Gelfond-Schneider folgt unmittelbar die Transzendenz der folgenden Zahlen:

Die Gelfond-Schneider-Konstante $2^{\sqrt {2}}$ sowie deren Quadratwurzel ${\sqrt {2}}^{\sqrt {2}}={\sqrt {2^{\sqrt {2}}}}$

Die Gelfond-Konstante $\,e^{\pi }$ , da $e^{\pi }=\left(e^{\mathrm {i} \pi }\right)^{\left(-\mathrm {i} \right)}=(-1)^{\left(-\mathrm {i} \right)}$ ist.

Die Zahl ${\mathrm {i} }^{\mathrm {i} }$ , die wegen ${\mathrm {i} }^{\mathrm {i} }=\left(e^{{\mathrm {i} }{\frac {\pi }{2}}}\right)^{\mathrm {i} }=e^{-{\frac {\pi }{2}}}={\frac {1}{\sqrt {e^{\pi }}}}$ eine reelle Zahl ist.

Die reelle Zahl ${\frac {\log 2}{\log 3}}$ ist transzendent, denn sonst erhält man durch Einsetzen von $a=3$ , $b={\frac {\log 2}{\log 3}}=\log _{3}{2}$ , da b notwendigerweise irrational ist, einen Widerspruch.

Mit dem Satz von Baker ergibt sich darüber hinaus die Transzendenz gewisser Zahlen, für die der Transzendenzbeweis aus dem Satz von Gelfond-Schneider heraus nicht zu leisten gewesen wäre. Dazu gehören beispielsweise:

${\sqrt {2}}\log 3 {\sqrt {3}}\log 5$
$\pi {\sqrt {2}}\log 7 {\sqrt {3}}\log 3$
$2^{\sqrt {2}}3^{\sqrt {3}}$

Siehe auch

Satz von Lindemann-Weierstraß
Vermutung von Schanuel, die diesen Satz verallgemeinert

Literatur

Alan Baker: Transcendental Number Theory. Cambridge University Press, London 1975, ISBN 978-0-521-20461-3 (Eintrag im Zentralblatt).
Peter Bundschuh: Einführung in die Zahlentheorie (= Springer-Lehrbuch). 2. Auflage. Springer Verlag, Berlin, Heidelberg, New York 1992, ISBN 3-540-55178-6, S. 241 ff., 270 ff.
Alexander Gelfond: On Hilbert's seventh problem. In: Doklady Akademii Nauk SSSR. Izvestija Akademii Nauk, Moskau 2.1934, S. 177–182. ISSN 0002-3264
Th. Schneider: Transzendenzuntersuchungen periodischer Funktionen. Bd. I. Transzendenz von Potenzen. In: Journal für die reine und angewandte Mathematik. de Gruyter, Berlin 172, 1935, S. 65–69. ISSN 0075-4102
Naum Iljitsch Feldman, Juri Walentinowitsch Nesterenko: Transcendental Numbers (= Encyclopedia of Mathematical Sciences. Band 44). Springer-Verlag, Berlin 1998, ISBN 3-540-61467-2 (MR1603604).
Theodor Schneider: Einführung in die transzendenten Zahlen (= Die Grundlehren der Mathematischen Wissenschaften. Band 81). Springer Verlag, Berlin, Göttingen, Heidelberg 1957.
Fridtjof Toenniessen: Das Geheimnis der transzendenten Zahlen. Eine etwas andere Einführung in die Mathematik. 2. Auflage. Springer, Berlin 2019, ISBN 978-3-662-58325-8, doi:10.1007/978-3-662-58326-5.